Normal Distribution
What is normal distribution
Due to Central Limit Theorem we have seen normal distribution really often.
The Normal distribution is one of the most important probability distributions in statistics, appearing frequently in nature and statistical theory.
Key Properties of Normal Distribution
- Definition: A bell-shaped, unimodal, and symmetric distribution
- Parameters: Characterized by two parameters:
- Mean (
): The center of the distribution - Standard Deviation (
) or Variance( ): The spread of the distribution
- Mean (
- Notation: If a variable follows a Normal distribution, it's denoted as X~ N(
, )
Standard Normal Distribution
The Standard Normal Distribution is a special case with:
- Mean = 0
- Variance = 1
- Denoted as X ∼ N(0, 1)
Standardizing Normal Variables
From your knowledge base:
- If X ∼ N(
), then Y = (X - μ)/σ ∼ N(0, 1) - This process is called standardizing a Normal variable
- The resulting value is known as a z-score
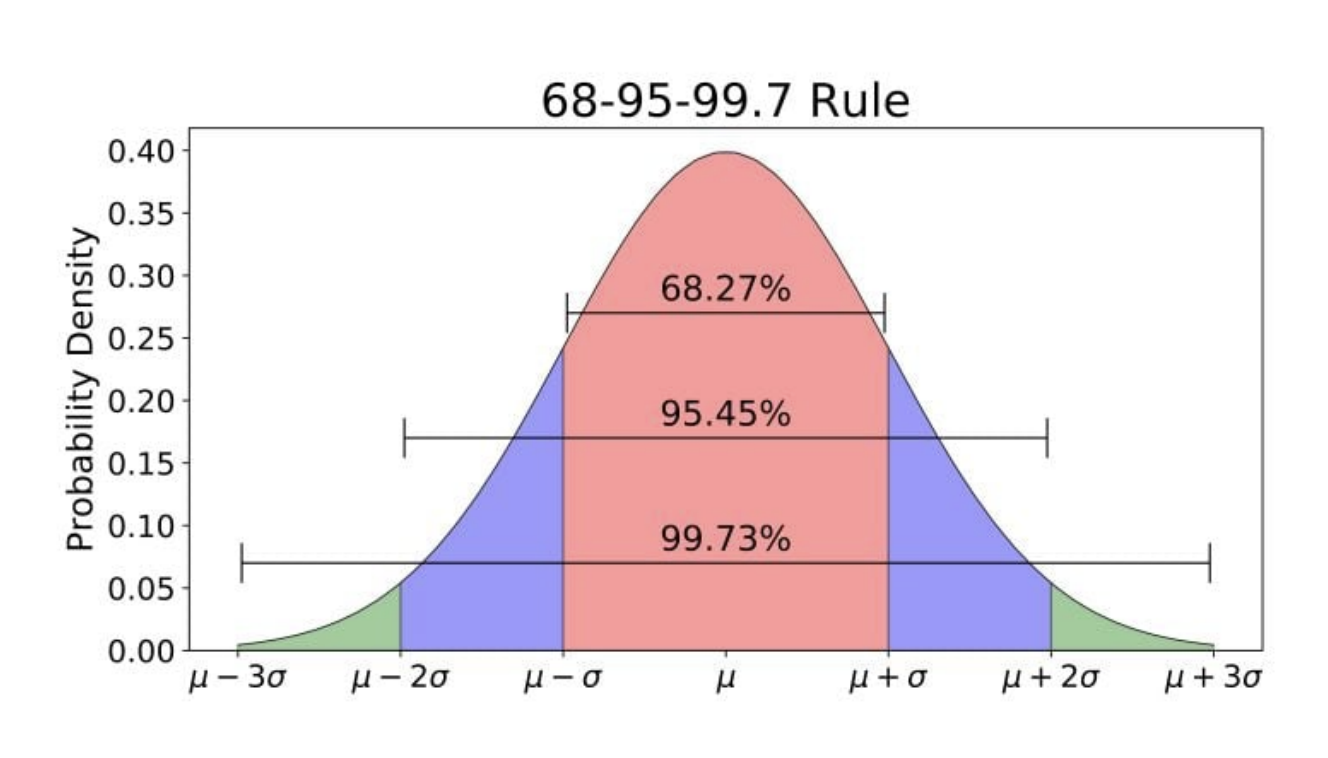
Important Probabilities
For a Standard Normal Distribution:
- P(|X| < 1) = 0.68286 (68% of values within 1 standard deviation)
- P(|X| < 2) = 0.9545 (95% of values within 2 standard deviations)
- P(|X| < 3) = 0.9973 (99.7% of values within 3 standard deviations)
- Also known as 68-96-99.7 Rule: